
그림 1. 세트!
Mark Baker et al. 은 2013년 세트 카드 덱을 가지고 할 수 있는 새로운 게임인 “세트, 플래닛, 코멧” 이라는 게임을 미국 수학 협회에 제안하였다. 이 게임은 가히 세트 확장판이라고 불리기에 손색이 없다.
12장의 무작위 카드들 중 세트가 없을 확률은 1/30이지만, 세트를 진행하다 보면 빠르게 떨어져서 1/13과 1/14 사이가 된다. 많이 보이는 광경이다. 사실 모든 게임들 중 약 70%는 중간에 세 장을 더 깔아야 한다고 알려져 있다. 하지만 세트, 플래닛, 코멧의 가장 큰 특징으로는 게임판 위에 세트가 존재하지 않아서 새로 까는 일이 없다는 점을 꼽을 수 있다. 세트를 해 본 사람은 이것이 굉장히 대단한 장점이라는 것을 곧바로 이해할 것이다.
나는 이 게임이 세트보다 훨씬 재밌다고 본다. 보통의 고인물 세트 게임보다 훨씬 느리게 진행된다는 점도 장점이다. 어렵다.
1. 플래닛이란?
이 게임의 룰을 설명하기 위해서는 먼저 세트에 대해 확실히 짚고 넘어갈 필요가 있다. 세트는 “4차원 3×3×3×3 modular 초입방체 안에서 직선을 찾는 게임" 이라고 말할 수 있겠다. 4차원은 조건 4개 (색깔, 음영, 모양, 개수) 를 말한다. 이해하지? 세트의 특징으로는, 두 개의 카드가 정해졌을 때 이 두 카드와 세트를 이루는 카드가 단 하나만 존재한다는 점을 꼽을 수 있다. 아주 중요한 특성이니 잘 기억하자. 이제 플래닛에 대해 설명해 보겠다.
세트가 한 직선 위에 있는 세 점이라면, 플래닛은 한 평면 위에 있는 네 점이다. 즉 카드 4장을 찾는데 이것이 하나의 평면 위에 있으면 된다. 플래닛에는 크게 두 종류가 있다. 첫 번째는 이미 완성된 세트에 아무 카드 하나가 더해진 모습 (3+1형). 그리고 두 번째는 세트를 포함하지 않는 모습(2+2형)이다. 첫 번째 경우가 왜 한 평면이 되는지는 다들 바로 이해할 것이라고 믿는다. 직선과 점이면 하나의 평면이 결정되기 때문이지. 그러나 두 번째 경우에 대해서는 조금 더 설명이 필요할 것이다. 아래와 같은 경우가 그 예시이다.
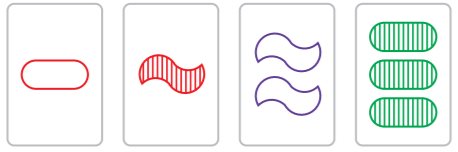
그림 2. (세트를 포함하지 않는) 플래닛!
이게 왜 플래닛이냐고? 그것은, 저 4장의 카드는 아래의 평면 안에 있기 때문이다. 놀랍지?

그림 3. 그림 2의 네 장의 카드를 포함하는 평면.
그러나 4장의 카드가 플래닛을 이루는 조건을 말로 설명하기는 쉽지 않을 것이다. 곰곰이 생각해 보면, 세트를 포함하지 않는, 즉 2+2형 플래닛은 이렇게 설명할 수 있다는 것을 알 수 있다.
"4장의 카드를 ㅡ 첫 2장과 세트를 이루는 카드와, 마지막 2장과 세트를 이루는 카드가 서로 같은 카드가 되도록 ㅡ 2장과 2장으로 분할할 수 있다면, 이 4장의 카드는 2+2형 플래닛을 이룬다. 역도 성립한다."
이는 아래의 그림에서 다시금 확인할 수 있다.
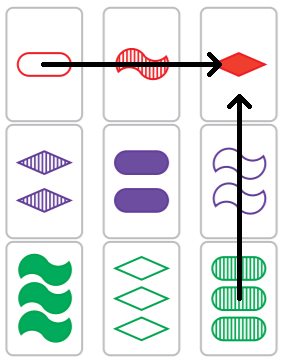
그림 4. 그림 2가 (2+2형) 플래닛임을 쉽게 아는 법.
평면에서 나타날 수 있는 플래닛의 다른 예시를 보자.
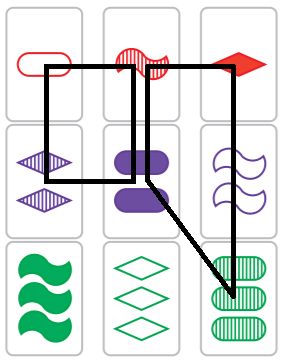
그림 5. 한 평면 위에서 나타날 수 있는 다른 2+2형 플래닛의 예시들.
직사각형의 경우 평행한 직선 2개로 나뉘기 때문에 같은 카드와 세트를 이루는 2장과 2장으로 분리를 못 하는 것 아니냐고? 틀렸다. X자로 두 장씩 묶어서 다시 보면, 나눠진 2장과 2장 모두 같은 카드(초록색 빗금 동그라미 3개)와 세트를 이룬다는 것을 확인할 수 있다.
2. 코멧이란?
이제 플래닛에 대해서는 설명이 된 것 같으니, 코멧이 뭔지를 알아보자. 아니, 알아보기 전에 세트에 대해서 다시 한 번 짚고 넘어가자. 3장의 카드가 세트를 이룬다는 것은, 색깔/음영/모양/개수 각각에 대해서 3개의 카드의 "합"이 0 (mod 3) 이 된다는 뜻이다. 무슨 소린지 이해했을 거라 믿는다. 각각의 조건에 대해 AAA, BBB, CCC, ABC 네 가지 경우가 있겠지. 그래서 아무 2장의 카드를 집으면 이 2장과 세트를 이루는 카드가 유일하게 결정되는 것이다.
이제 코멧을 설명해 보자. 코멧은 "더해서 합이 0 (mod 3)이 되는 9장의 카드" 를 말한다. 쉽지? 그래서 8장이 주어지면 이 8장과 코멧을 이루는 카드가 유일하게 결정된다. 다만, 세트의 경우 세 번째 카드는 반드시 앞의 두 카드와 다른 카드가 되지만 코멧의 경우 그건 성립하지 않는다. 즉, 주어진 8장의 카드와 코멧을 이루는 한 장의 카드가 이미 주어진 8장의 카드 중 하나일 수도 있는 것이다.
쉽게 생각하면, 9장을 무작위로 꺼냈을 때 코멧일 확률은 아마 1/81 근처일 것이다. (정확한 확률은 알려지지 않았다.) 그냥 머릿속으로 세트 카드를 하나 상상하면서 카드를 뽑았을 때 정확히 맞출 확률이 1/81이니까, 딱 그 정도로 보기 힘들다는 얘기다.
3. 그래서 세트, 플래닛, 코멧의 룰은?
세트와 비슷하게 진행되지만, 9장의 카드만 가지고 진행한다는 차이점이 있다. 플레이어는 세트, 플래닛, 코멧 중 하나를 발견했을 경우 조합의 이름을 외치고 가져가면 된다. 세트와 마찬가지로 장수를 유지하다가 덱이 다 떨어져 보충이 불가능한데 더 이상 발견되는 조합이 없다면 게임을 종료한다. 가져간 장수가 그대로 점수가 된다.
플래닛과 코멧은 발견하기 더 어렵지만, 발견했다면 더 많은 카드를 한 번에 가져갈 수 있으므로 그만큼의 메리트가 있는 셈이다. 코멧은 발견하기는 굉장히 어려운데 발견하면 9점이라는 점에서 약간 조커 같은 느낌으로 존재하는 것 같다. 다만 앞에서 말했듯이 플래닛은 완성된 세트를 포함하는 3+1형일 수도 있는데, 발견한 플래닛이 이런 종류라면 세트만 가져가는 것으로 특수 룰이 정해져 있다.
앞에서도 말했지만 이 게임의 경우 9장을 어떻게 깔든 반드시 세트, 플래닛, 코멧 중 하나는 존재하기 때문에 세트처럼 추가로 3장을 깐다거나 하는 일이 없다는 것이 특수한 점이다. 이 사실은 컴퓨터로 전수조사를 해서 알아냈다고 한다. 가령 다음과 같이 플래닛을 포함하지 않는 9장의 카드가 깔린 경우, (플래닛이 세트를 포함하는 개념이니까, 플래닛이 없다는 말은 세트도 없다는 말이다.) 이 9장의 카드는 틀림없이 코멧일 것이다.

그림 6. 플래닛이 없는 9장. 플래닛이 없으므로 이 9장의 카드는 코멧이다.
하지만 임의의 9장의 카드가 플래닛을 포함하지 않을 확률은 0.00523...%, 즉 약 1/19117이다. 세트에서 임의의 15장 중 세트가 없을 확률이 1/2700임을 고려한다면 정말 마주치기 어려운 상황이라는 뜻이다. 물론 임의의 15장과, 12장 안에 세트가 없어서 3장을 더 깔아 만들어진 15장은 확률이 다르다. 후자는 1/88이다. 이것도 거의 볼 일 없는 상황인데 플래닛이 없는 9장을 본다는 건 과장 좀 보태서 준 로또급 아닐까?
다만 필자는 감점에 대한 룰을 추가로 제안하고 싶다. 세트는 틀렸을 경우 -1점이지만, 세트, 플래닛, 코멧은 틀렸을 경우 어떻게 되는지 제시되어 있지 않다. 틀렸을 경우 외친 조합의 장수만큼 감점하는 것이 어떨까 한다.
그리고, 세트는 20장을 깔아야 항상 존재하지만, 플래닛은 10장만 깔아도 항상 존재한다. 코멧을 배제한 게임을 하고 싶다면 장수를 10장으로 변형하고 코멧 규칙을 없앤 채 플레이하는 것은 어떨까?
4. 너무 어려워요
맞다. 이거 겁나 어렵다. 따라서 (2+2형) 플래닛의 유형에 대해 조금 더 설명해 보고자 한다.
먼저, 2+2형 플래닛은 절대로 3장과 1장으로 나누어질 수 없다. 만약 당신이 동그라미 3개와 물결표 1개를 보고 있다면 이 4장은 2+2형 플래닛이 아니다. 물론 3+1형 플래닛일 수는 있지만... 걱정하지 마라. 이 노트를 읽는 당신은 세트 고인물이기 때문에, 당신이 4장을 놓고 플래닛인지 아닌지 고민하고 있다면 그 4장 중에는 세트가 없다. 있으면 이미 발견했다.
아무튼, 이를 간단히 표현하면 2+2형 플래닛은 AAAB와 같은 유형은 나타날 수 없다는 말이다. 따라서 2+2형 플래닛은 AAAA, ABCC, AABB 세 가지 유형만 나타날 수 있다. 당신이 체크하고 있는 4장의 카드가 AAAA형이라면, 아주 좋다. 당신은 이제 4차원이 아니라 3차원에서 생각할 수 있고, 계속해서 다른 조건을 체크하면 된다.
당신이 체크하고 있는 4장의 카드가 ABCC형이라면, 이는 반드시 AB|CC로 나누어야 한다는 말이 된다. AC|BC로 나누면 각 조합이 같은 카드와 세트를 이룰 수 있을 리 없기 때문이다. 이제 어떻게 나눠서 봐야 하는지 알았으니 각 조합이 같은 카드와 세트를 이루는지 보면 된다.

그림 7. 1233형. 이 4장이 플래닛이라면, 반드시 검빗|흰흰으로 나눠질 것이다.
AABB형이 가장 어렵다. 왜냐면 다음 그림과 같이 정말정말 AABB형처럼 생겨먹었음에도 불구하고 플래닛을 이루지 않는 경우가 있기 때문이다. 순서대로 AABB라고도, ABAB라고도, ABBA라고도 표현될 수 있는 경우 이렇게 된다.
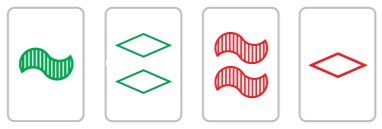
그림 8(a). 1122형. 하지만 플래닛이 아니다.
반면 다음 경우는 플래닛이다. 순서대로 AABB와 ABAB로는 표현되지만 ABBA로 표현되지 않기 때문이다. 이 두 가지를 빠르게 구분하는 방법은 필자도 아직 모르겠다. 알아내면 알려줘라.
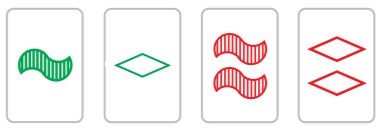
그림 8(b). 1122형. 위와 다르게, 이것은 플래닛이다. 14와 23을 묶어 보자.
그리고 코멧의 경우, 만약 어떤 조건에 대해서 9장의 합이 0 (mod 3)이라면, 반드시 AAA/BBB/CCC/ABC 조합 3개로 나눌 수 있다. 역도 성립한다. 그러니까 코멧을 체크할 때는 일일이 숫자로 치환해서 더해서 3으로 나누는 식으로 체크하지 말고, 4가지의 조건 각각에 대해서 3장씩 묶어서 옆으로 치워 가면서 체크하는 방법이 있다.
좀 더 코멧을 빠르게 찾고 싶다면, 이걸 외워라: <441, 522, 711>. 사실 코멧을 체크할 때 각 조건에 대해서 카드를 같은 종류끼리 세 묶음으로 나눴을 때, 딱 여섯 가지 조합만이 코멧이다. 같은 종류끼리 a개 b개 c개로 나눠진다고 할 때, (a,b,c) = (9,0,0), (6,3,0), (3,3,3), (4,4,1), (5,2,2), (7,1,1) 이 그것이다. 이 글을 여기까지 읽고 있으면 당신은 똑똑이기 때문에 900, 630, 333 케이스는 보자마자 알 것이고, 비직관적이라 따져봐야 하는 경우가 441 522 711 세 가지다. 이제 실전에서 코멧을 찾을 때 네 가지 조건이 이 순서쌍을 각각 만족하는지를 체크해 보고, 네 조건 모두가 순서쌍을 만족한다면 코멧이라고 외치면 된다. 자기 눈에 쉽게 보이는 조건부터 확인하면 되는데, 필자는 음영, 색깔, 개수, 모양 순서로 확인하는 편이다.
즐거운 세트, 플래닛, 코멧 되시길!
출처: Mark Baker et al., "Sets, Planets, and Comets."
이충명, 2020.04.29.
뒤로가기 ◁
뒤로가기 ◁